Union-find Disjoint set
Union-find Disjoint set (UFDS) is an abstract data structure that simulates a collection of elements belongs to a collection of sets, where we need to support the following two operations
- Determine if two element belongs to same set,
- Combine two disjoint set.
Linked list Implementation
We would want to support the above operation with decent efficiency. The main paradigm for supporting such data structure is to choose one unique element to represent the set.
Then, a naïve approach would be using a linked list, where each node contains a parent pointer points back to the head, which is used to represent the set. It gives constant time to determine if two element belongs to same set by looking up the parent pointer's address of this two element.
To combine two disjoint sets, denote set S1 and set S2. The operation would be choice one set from set S1, set S2 to be merged and let opposite one represent the new set. For example, we let set S2 to be merged, set S1 become new set, then we would change all nodes' parent pointer in set S2 to set S1's head, and then combine the two linked list, as shown by the diagram. This operation will take Θ(length of S1 or S2) depend on which set2.
Combine - size resolution
As one can observe above, while determine same set will have constant running time, the combine operations takes operation linearly to the length of linked list. In order to maximise efficiency, we would always want to merge the shorter length linked list to the longer ones. We can store an additional attribute, denote size so that we have constant time for look up the size of set. With length, we reduce time complexity to Θ(MIN(S1, S2)).
By using this additional size, it can boost time efficiency for our data structure. Consider the following scenario, suppose there are initially n elements each contained in n disjoint sets, then n of combine operation will takes Θ(nlog(n))time. To prove this time complexity is true, we consider one arbitrary sets denote S1 and operation spend on this set. For each combination step between S1 and S2 (a random set), the resulting is either1. S1's pointer being updated, then the result new set's size is strictly greater than length of S1, this takes Θ(S1),2. S1's pointer not being updated, then takes no operation.What this means, is that for x's size <= n, each object's pointer being updated for at most O(log(n)) times, and the total time complexity for above operations will be O(nlog(n)).
typedef struct set *Set;
struct set {
int val;
Collection head;
Set next;
};
struct collection {
Set first;
Set last;
int size;
};
// Check two set's parent pointer's address
bool isSameSet(Set a, Set b) {
return a && b && a->head == b->head;
}
// Merge two set, u,v can be still used
void Union(Set a, Set b) {
// UNION being done
if (a->head == b->head) return;
// Compare the size, always choice merge smaller set to a bigger set
int sizeA = a->head->size;
int sizeB = b->head->size;
Set appendedSet = sizeA >= sizeB ? b->head->first : a->head->first;
Collection appendedColl = sizeA >= sizeB ? a->head : b->head;
Collection destroyedColl = sizeA >= sizeB ? b->head : a->head;
// Modify the size
appendedColl->size += destroyedColl->size;
// Change appendedSet's new head
while (appendedSet != NULL) {
appendedSet->head = appendedColl;
appendedSet = appendedSet->next;
}
// Merge two list
appendedColl->last->next = destroyedColl->first;
appendedColl->last = destroyedColl->last;
free(destroyedColl);
}
As one can observe above, while determine same set will have constant running time, the combine operations takes operation linearly to the length of linked list. In order to maximise efficiency, we would always want to merge the shorter length linked list to the longer ones. We can store an additional attribute, denote size so that we have constant time for look up the size of set. With length, we reduce time complexity to Θ(MIN(S1, S2)).
By using this additional size, it can boost time efficiency for our data structure. Consider the following scenario, suppose there are initially n elements each contained in n disjoint sets, then n of combine operation will takes Θ(nlog(n))
time. To prove this time complexity is true, we consider one arbitrary sets denote S1 and operation spend on this set. For each combination step between S1 and S2 (a random set), the resulting is either
1. S1's pointer being updated, then the result new set's size is strictly greater than length of S1, this takes Θ(S1),
2. S1's pointer not being updated, then takes no operation.
What this means, is that for x's size <= n, each object's pointer being updated for at most O(log(n)) times, and the total time complexity for above operations will be O(nlog(n)).
typedef struct set *Set;
struct set {
int val;
Collection head;
Set next;
};
struct collection {
Set first;
Set last;
int size;
};
// Check two set's parent pointer's address
bool isSameSet(Set a, Set b) {
return a && b && a->head == b->head;
}
// Merge two set, u,v can be still used
void Union(Set a, Set b) {
// UNION being done
if (a->head == b->head) return;
// Compare the size, always choice merge smaller set to a bigger set
int sizeA = a->head->size;
int sizeB = b->head->size;
Set appendedSet = sizeA >= sizeB ? b->head->first : a->head->first;
Collection appendedColl = sizeA >= sizeB ? a->head : b->head;
Collection destroyedColl = sizeA >= sizeB ? b->head : a->head;
// Modify the size
appendedColl->size += destroyedColl->size;
// Change appendedSet's new head
while (appendedSet != NULL) {
appendedSet->head = appendedColl;
appendedSet = appendedSet->next;
}
// Merge two list
appendedColl->last->next = destroyedColl->first;
appendedColl->last = destroyedColl->last;
free(destroyedColl);
}Rooted Tree Implementation
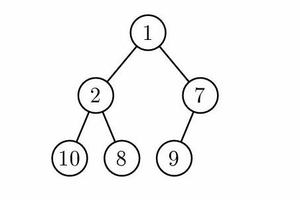
If we develop further on the idea of choosing one unique element to represent the set. A more efficient way would be using a general tree-like structure, with the root of tree used to representing the set. And general tree-like structure will be implemented using an array.

Rooted Tree implemented by array
Then, to determine if two set are equal, we will need to find the root of two set by recursively visit it's parent and finally we would compare the root.
If we want to combine two set, choice the root to represent the new set and simply points the merged ones to the new root. As shown by the diagram.
If we develop further on the idea of choosing one unique element to represent the set. A more efficient way would be using a general tree-like structure, with the root of tree used to representing the set. And general tree-like structure will be implemented using an array.
 |
Rooted Tree implemented by array |
Then, to determine if two set are equal, we will need to find the root of two set by recursively visit it's parent and finally we would compare the root.
If we want to combine two set, choice the root to represent the new set and simply points the merged ones to the new root. As shown by the diagram.
Combine - rank resolution
Similar idea can be also apply to rooted tree implementation, when combine two sets, we would want the root of the tree with fewer node points to the root with more nodes. To do so, we can store an additional attribute **rank** for each of nodes, that indicate upper bound of the height of the node.
class UnionFind {private: vector<int> p, rank;public: // Constructor UnionFind(int N) { p.assign(N, 0); for (int i = 0; i < N; i++) { p[i] = i; } }
// Supported Operation int findSet(int i) { return p[i] == i ? i : findSet(p[i]); } bool isSameSet(int i, int j) { return findSet(i) == findSet(j); } void unionSet(int i, int j) { int x = finSet(i), y = findSet(j); if (rank[x] > rank[y]) { p[y] = x; } else { p[x] = y; } if (rank[x] == rank[y]) rank[y]++; }};
Similar idea can be also apply to rooted tree implementation, when combine two sets, we would want the root of the tree with fewer node points to the root with more nodes. To do so, we can store an additional attribute **rank** for each of nodes, that indicate upper bound of the height of the node.
class UnionFind {
private:
vector<int> p, rank;
public:
// Constructor
UnionFind(int N) {
p.assign(N, 0);
for (int i = 0; i < N; i++) {
p[i] = i;
}
}
// Supported Operation
int findSet(int i) {
return p[i] == i ? i : findSet(p[i]);
}
bool isSameSet(int i, int j) {
return findSet(i) == findSet(j);
}
void unionSet(int i, int j) {
int x = finSet(i), y = findSet(j);
if (rank[x] > rank[y]) {
p[y] = x;
}
else {
p[x] = y;
}
if (rank[x] == rank[y]) rank[y]++;
}
};
Combine - path compression
Idea of path compression is when we inspect the path denote P, from some node to it's root, we makes the node directly to the root. By doing so, it reduce the path from node to the parent. The following image shows this operation would do.
Path Compression
To achieve the above idea, we change our findSet function slightly. As it recurses, it makes a path between node and it's root, and as it rewinds back, it will update node's parent directly to the root.
int findSet(int i) { // Base case, reach the root if (p[i] == i) return i; // Recursive case p[i] = findSet(p[i]); // Rewind, pass back the root return p[i];}
As a result of above improvement, for m is number of disjoint-set operation, n is number of elements, the worst-case running time will be O(m * a(n)) where a(n) is a very slowly growing function, namely the inverse Ackermann function. Further detail can be found in CLRS Chapter 21.4.
Idea of path compression is when we inspect the path denote P, from some node to it's root, we makes the node directly to the root. By doing so, it reduce the path from node to the parent. The following image shows this operation would do.
 |
| Path Compression |
To achieve the above idea, we change our findSet function slightly. As it recurses, it makes a path between node and it's root, and as it rewinds back, it will update node's parent directly to the root.
int findSet(int i) {
// Base case, reach the root
if (p[i] == i) return i;
// Recursive case
p[i] = findSet(p[i]);
// Rewind, pass back the root
return p[i];
}
As a result of above improvement, for m is number of disjoint-set operation, n is number of elements, the worst-case running time will be O(m * a(n)) where a(n) is a very slowly growing function, namely the inverse Ackermann function. Further detail can be found in CLRS Chapter 21.4.