Fracturing Search

-
Have you ever had that insatiable urge to find the kth smallest minimum spanning subtree which of a weighted graph? (I know I have) Well look no further! This post will an exploration of fracturing search and its applications.

(No prerequisite knowledge it required to understand the concepts, although it will be helpful graph theory terminology and an algorithm that solves the standard minimum spanning tree problem.)

An example - finding the kth smallest value in a heap


Fracturing search is a method that partitions your search space, and explores it in a way to get the "kth best" item. Let me illustrate with an example:

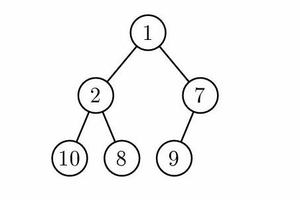
Lets consider a heap, which is a binary tree where the value of a parent is always strictly smaller than the value of any child (this property is known as the heap invariant). For example, 1 < 2 and 1 < 7, because (1) is the parent of (2) and (7).


We want to find the kth smallest value. Now is a good time to pause and think if you want to try it yourself.



Due to our heap invariant, the 1st smallest value is always the root. More generally, the smallest value of a tree is always the root node. I shall depict this idea in blue from now on. (In practice you would implement this as a function that takes a subtree and returns the smallest value - the root).


Hence we can say that the 2nd smallest value is the smallest value of the left subtree or the smallest value of the right subtree, namely 2 or 7. It is clear that the 2nd smallest value is 2.


Then the 3rd smallest value is the smallest value of the remaining subtrees, namely 10, 8 or 7. Hence we conclude the the 3rd smallest value is 7.



This process looks like "fracturing" our tree into smaller trees, hence the name Fracturing Search.

Solution - finding the kth smallest value in a heap


#include <bits/stdc++.h>
using namespace std;


int N, K, heap[1000005];

struct Subtree {
	// every subtree can be uniquely represented its root node
	// note that the minimum node is the root node, with a value of `heap[root]`
	int root;
	
	// given another subtree return which one is minimum
	// this is useful for priority queue shenanigans
	bool operator<(Subtree other) const {
		return heap[root] > heap[other.root];
	}

	// a partition of a tree returns the left subtree and right subtree
	vector<Subtree> getPartition() {
		vector<Subtree> output;
		// left child
		if (2 * root <= N) output.push_back({2 * root});
		// right child
		if (2 * root + 1 <= N) output.push_back({2 * root + 1});
		return output;
	}
};


signed main() {
	// N = total number of nodes in the tree
	cin >> N;

	// K = we want the kth minimum node
	cin >> K;
	assert(1 <= K && K <= N);

	// read in the tree as a standard heap structure
	//  - 1 is the root
	//  - 2*node is the left child of nod
	//  - 2*node+1 is the right child of node
	for (int i = 1; i <= N; ++i) {
		cin >> heap[i];
	}

	priority_queue<Subtree> pq;
	// initially searching the whole tree, i.e. the tree which has 1 as the root
	pq.push({1});

	for (int ithBest = 1; ithBest < K; ++ithBest) {
		Subtree curr = pq.top();
		pq.pop();
		for (Subtree partition : curr.getPartition()) {
			pq.push(partition);
		}
	}
	int ans = pq.top().root;
	printf("The %dth smallest node is %d, with a value of %d\n", K, ans, heap[ans]);
}

The illustrated example is equivalent to the input

6 3
1 2 7 10 8 9


This algorithm can also be applied to most problems which gives you many states, each which a particular value, and asks for the state with the kth smallest value. (given that you can easily find the minimum of a subset of states, and that you can partition a subset of states efficiently).

Try it yourself - kth smallest spanning tree

Try the kth smallest spanning tree problem, here's some starter code.

int main() {
    // STATEMENT:
    // Given an undirected weighted graph, find the total costs of the minimum 
    // spanning subtree to the kth minimum spanning subtree

    // CONTRAINTS:
    // N, M, K <= 2000
    // K <= number of possible spanning trees
    // 1 <= a_i, b_i <= N
    // 0 <= w_i
    // \sum_i w_i <= INT_MAX

    // INPUT FORMAT:
    // N M K
    // a_1 b_1 w_1
    // ...
    // a_M b_M w_M
    cin.tie(0); ios::sync_with_stdio(0);
    
    cin >> N >> M >> K;
    for (int i = 0; i < M; ++i) cin >> edges[i].second.first >> edges[i].second.second >> edges[i].first;
    sort(edges, edges + M);

    fracturingSearch();
    //bruteForce();
}

Solutions - kth smallest spanning tree



And here's my solution in the better language (eww Java 🤢🤮)
#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
#include <assert.h>
using namespace std;

int N, M, K;
pair<int, pair<int, int>> edges[2005];
int parents[2005];

//////////////////////////////////////////////////////////////////////
void clearDSU() {
    for (int node = 1; node <= N; ++node) parents[node] = node;
}

int getParent(int node) {
    if (parents[node] == node) return node;
    return parents[node] = getParent(parents[node]);
}

bool doUnion(int a, int b) {
    int pA = getParent(a), pB = getParent(b);
    bool ans = (pA == pB);
    parents[pA] = pB;
    return ans;
}

bool doUnion(pair<int, int> edge) {
    return doUnion(edge.first, edge.second);
}

// find whether all nodes are in the same component
bool isMerged() {
    for (int node = 1; node <= N; ++node) {
        if (getParent(node) != getParent(1)) return false;
    }
    return true;
}

//////////////////////////////////////////////////////////////////////

struct State {
    int cost = 0;
    vector<int> choices;
    vector<bool> used;

    State(int M) {
        choices.resize(M);
        used.resize(M);
    }

    bool operator<(State o) const {
        return cost > o.cost;
    }
};
priority_queue<State> pq;

State initState() {
    State output(M);

    clearDSU();
    for (int i = 0; i < M; ++i) {
        if (!doUnion(edges[i].second)) {
            output.cost += edges[i].first;
            output.used[i] = true;
        }
    }
    return output;
}

State findNeighbour(vector<int> choices) {
    State output(M);
    output.choices = choices;

    clearDSU();
    for (int i = 0; i < M; ++i) {
        if (choices[i] == 1) {
            doUnion(edges[i].second);
            output.cost += edges[i].first;
            output.used[i] = true;
        }
    }
    for (int i = 0; i < M; ++i) {
        if (choices[i] == 0 && !doUnion(edges[i].second)) {
            output.cost += edges[i].first;
            output.used[i] = true;
        }
    }
    return output;
}

void fracturingSearch() {
    pq.push(initState());
    for (int rep = 0; rep < K; ++rep) {
        if (pq.empty()) {
            cout << -1 << "\n";
            continue;
        }

        State curr = pq.top();
        pq.pop();
        cout << curr.cost << "\n";

        for (int remIndex = 0; remIndex < M; ++remIndex) {
            // this edge is being used, but it could be swapped out
            if (curr.used[remIndex] && curr.choices[remIndex] == 0) {
                vector<int> newChoices = curr.choices;
                for (int i = 0; i < remIndex; ++i) {
                    if (curr.used[i]) newChoices[i] = 1;
                }
                newChoices[remIndex] = -1;

                State neighbour = findNeighbour(newChoices);
                if (isMerged()) pq.push(neighbour);
            }
        }
    }
}

void bruteForce() {
    vector<int> ans;
    for (int bits = 0; bits < (1 << M); ++bits) {
        int cost = 0;
        bool valid = true;

        clearDSU();
        for (int i = 0; i < M; ++i) {
            if (bits & (1 << i)) {
                if (doUnion(edges[i].second)) valid = false;
                cost += edges[i].first;
            }
        }
        if (valid && isMerged()) ans.push_back(cost);
    }

    sort(ans.begin(), ans.end());
    for (int i = 0; i < K; ++i) cout << (i < ans.size() ? ans[i] : -1) << "\n";
}


Bonus question!


And here's my solution (though I suggest you only look at this after trying the problem yourself):

/* N <= 2e3, K <= 2e3

fracturing search
O(NK log NK)
*/

#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
#include <assert.h>
using namespace std;
typedef long long ll;

ll N, K, D;
vector<ll> costs[2005];

struct State {
    ll numItems = 0, cost = 0;
    ll hasChoice;
    ll lastChoice;
    // choices[i] <= used[i]
    // day is discarded when used[d] = choices[d] = cost[d].size()
    // day has free choice when choices[d] = -1

    bool operator<(State o) const {
        if (numItems == o.numItems) return cost > o.cost;
        return numItems < o.numItems;
    }
};
priority_queue<State> pq;

State initState() {
    State output;
    output.numItems = D;
    for (ll d = 1; d <= D; ++d) output.cost += costs[d][0];
    output.hasChoice = 1;
    //output.used.resize(D + 1);

    return output;
}

void fracturingSearch() {
    pq.push(initState());

    for (ll rep = 0; rep < K - 1; ++rep) {
        State curr = pq.top();
        pq.pop();

        for (ll d = curr.hasChoice; d <= D; ++d) {
            //cerr << "d " << d << "\n";
            //cerr << "PQ size: " << pq.size() << "\n";
            // option 1: increment the cost
            for (ll itemI = 1; itemI < (ll)costs[d].size(); ++itemI) {
                State neighbour = curr;
                neighbour.cost += costs[d][itemI] - costs[d][0];
                neighbour.hasChoice = d + 1;
                //neighbour.used[d] = itemI;
                pq.push(neighbour);
            }

            // option 2: remove this day
            if (0 != (ll)costs[d].size()) {
                State neighbour = curr;
                neighbour.cost -= costs[d][0];
                neighbour.numItems--;
                neighbour.hasChoice = d + 1;
                //neighbour.used[d] = costs[d].size();
                pq.push(neighbour);
            }
        }
    }

    cout << pq.top().numItems << " " << pq.top().cost << "\n";
}

int main() {
    cin.tie(0); ios::sync_with_stdio(0);

    cin >> N >> K >> D;
    for (ll d, w, i = 0; i < N; ++i) {
        cin >> d >> w;
        costs[d].push_back(w);
    }
    for (ll d = 1; d <= D; ++d) sort(costs[d].begin(), costs[d].end());

    fracturingSearch();
}

Popular posts from this blog

Tips for Competitive Programming

-
Image
Competitive programming is by no means easy, I struggled with it for a long time. In this post I want to provide some helpful tips, which will hopefully be helpful to you at any stage in your competitive programming journey. How do I read problems? Read all the problems It is not always the case that the first problem is the easiest, because it cannot be assumed that problems are in difficulty order. Even if it was in "difficulty order", what the tutors think is difficult may be different from what you think is difficult. Read all the subtasks (this doesn't apply for contests such as ICPC) Subtasks help guide you towards observations and partial solution by presenting helpful subproblems. Note that this isn’t...
Read more

Implementation tips for competitive programming

-
Implementation tips for competitive programming It’s uncommon for code you write to work properly the first time you run it. And if you’re not careful, you can spend hours debugging and still be left with code that doesn’t work. This is especially problematic in ICPC, when you have only one computer between three people. Below are a few tips on how to improve the implementation and debugging process.  Before you start implementing Proving your solution Once you have a solution, the first step is to convince yourself it is correct. If you skip this step, you could invest a lot of time into coding only to later realise that your entire idea is incorrect. You don’t need a formal mathematical proof, just enough that you are sure it works. When doing this, try to think about the worst cases which could break your algorithm, and then reason why they do or do not.  Planning your code Once you are sure you have a correct solution, the next st...
Read more

The Art of Making Programming Problems

-
Image
Hello! Today we’ll explore the wonderful world of creating problems for programming contests. This article could be used as a sort of guide if you’re interested in writing problems yourself, but it’s intended for anyone interested in the process or philosophy behind making problems.   The scope of the article is quite broad, and in its four parts, we will discuss (1) why to make programming problems, (2) how to invent problems, (3) how to plan a contest, and (4) how to prepare problems. Do feel free to skip around if any of these topics tickle your fancy, or if you’re up for it, I invite you to read the article through from top to bottom. A lot of the thoughts presented here are based on my own modest experience with problem setting, mainly for university contests, informatics olympiads and miscellaneous educational purposes. Keep in mind that nothing I say is meant to prescribe a correct way to do things, just to describe what I’ve personally found effective for the work I’ve done...
Read more

Interactive Tasks

-
Interactive tasks are tasks where your code interacts with another program, often called a grader , rather than simply reading input and printing output. Due to this novel format, people are often scared off and avoid attempting these problems. My goal in this blog is to remove your fear towards interactive tasks. Example Let's start with a basic example, Guess the Number , which you can view in more detail here . There is some hidden number and you have to interactively guess it. The hidden number is always an integer from 1 to 1000000.  You can make queries to the grader. Each query is an integer from 1 to 1000000. There are two different responses the grader can provide: "<" (without quotes), if the hidden number is less than the integer in your query, ">=" (without quotes), if the hidden number is greater than or equal to the integer in your query. When your program wants to guess the hidden number, print "! x" (without quotes), where x is th...
Read more

Sqrt linked lists

-
Image
I present a (novel?) variation of a linked list, which allows for insertion, deletion and querying in worse case O(sqrt(n)) If these things interest you, you may like to look at: big O notation, otherwise known as time complexity. This is a useful method to measure how fast things are, rather than looking at the number of "steps" in the worse case. https://onecore.tech/informatics/5 skip lists, a similar variation with a randomised aspect. It is faster than mine in the average case, but slower in the worse case. https://en.wikipedia.org/wiki/Skip_list B-trees, which although are not linked lists, are faster than mine in all cases. Not to be confused with binary trees. https://en.wikipedia.org/wiki/B-tree // Written by Ryan Ong (z5419383) // on 14/04/2022 /** * Sqrt Linked List! * I want to answer these queries in about sqrt(n) steps: * - "insert this value at index i" * - "remove the value at index i" * - "what is the value ...
Read more

Introduction to Dynamic Programming

-
Image
This is a quick 5 minute easy-to-read programme, for even the least experienced programmers. So you wanna see c some new programming, or some new epic pro-gamer move s to up your competitive programming skills. Well, look no further with this CPMsoc blog on dynamic programming! Well, the obvious question is what is dynamic programming? Dynamic programming is programming that is dynamic. A quick google search would reveal (or at least according to Programiz), " technique in computer programming that helps to efficiently solve a class of problems that have overlapping subproblems and optimal substructure property ." What does this actually mean though? The paramount idea regarding dynamic programming circulates around the idea of sub-programs; essentially taking a large problem and breaking it down into smaller problems. Then, the values of the smaller-problems are saved to be used later to solve the initial, larger problem. Accordingly, the key benefit of dynamic programmin...
Read more

Introduction to Competitive Programming

-
Introduction to Competitive Programming  Have you heard your friends talk about LeetCode or Codeforces contests? Maybe you’re wondering what competitive programming is all about. Here’s what you need to know. What is Competitive Programming? Competitive Programming (CP, or sometimes known as Informatics) is an activity where we try to solve clearly defined computational problems using code. The 'competitive' part of CP comes from the numerous contests where people aim to correctly solve as many problems as possible in a fixed timeframe, typically around two to five hours. Solutions must also follow time and memory constraints which means your code needs to be both correct and efficient. These problems are thought to train and test you in three related areas: Problem solving . Algorithms and data structures , which we apply to solve problems efficiently. Implementation , the process of writing and testing code. Many people participate in competitive programming for the challeng...
Read more

Union-find Disjoint set

-
Image
Union-find Disjoint set (UFDS) is an abstract data structure that simulates a collection of elements belongs to a collection of sets, where we need to support the following two operations Determine if two element belongs to same set, Combine two disjoint set. Such a data structure can be helpful in situation such as finding connected component of a diagram, for example Kruskal's algorithm. Linked list Implementation We would want to support the above operation with decent efficiency. The main paradigm  for supporting such data structure is to choose one unique element to represent the  set. Then, a naïve approach would be using a linked list, where each node contains a  parent pointer points back to the head, which is used to represent the set . It gives  constant time to determine if two element belongs to same set by looking  up the parent pointer's address of this two element. To combine two disjoint sets, denote set S1 and set S2 . The operation would be c...
Read more